机器学习经典算法：决策树（2）

数据科学工厂

1. 概述

决策树（Decision Tree）是有监督学习中的一种算法，并且是一种基本的分类与回归的方法。决策树有两种：分类树和回归树。

决策树是用于分类和回归的工具，它将数据特征值拆分为决策节点处的分支（例如，如果特征是一种颜色，则每种可能的颜色都会成为一个新分支），直到做出最终决策输出。
一般来说，决策树只是一个嵌套 if-else 条件的结构。在数学上，决策树使用平行于任何一个轴的超平面将坐标系切割成超长方体。

树形结构

2. 构建

过程包括：特征选择、决策树的生成和决策树的剪枝

特征选择

标准：希望决策树的分支节点所包含的样本尽可能属于同一类别，也就是节点的纯度（purity）越来越高。

下面三个图表示的是纯度越来越低的过程，最后一个表示的是纯度最低的状态。

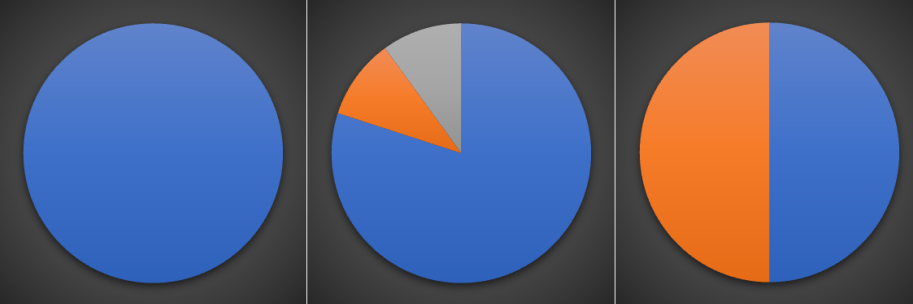
度量不纯度的指标有很多种，比如：熵、增益率、基尼指数。本文使用熵（香农熵）

香农熵

熵定义为信息的期望值。在信息论与概率统计中，熵是表示随机变量不确定性的度量。假定当前样本集合D中一共有n类样本，第i类样本为，那么的信息定义为：

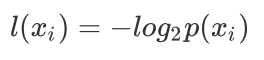
其中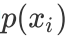是选择该分类的概率。通过上式，我们可以得到所有类别的信息。为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值(数学期望)，通过下面的公式得到：

值越小，则D的不纯度就越低。

"""
    函数功能：计算香农熵
    参数说明：
        dataSet：原始数据集
    返回：
        ent:香农熵的值
"""
def calEnt(dataSet):
    n = dataSet.shape[0] #数据集总行数
    iset = dataSet.iloc[:,-1].value_counts() #标签的所有类别
    p = iset/n #每一类标签所占比
    ent = (-p*np.log2(p)).sum() #计算信息熵
    return ent

信息增益

信息增益（Information Gain）的计算公式其实就是父节点的信息熵与其下所有子节点总信息熵之差。

信息增益的计算公式为：

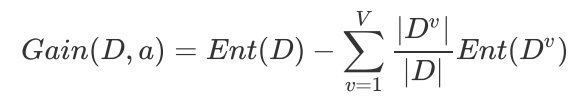
3. 递归构建

ID3

构建决策树的算法有很多，比如ID3、C4.5和CART，本文选择ID3算法。

def createTree(dataSet):
    featlist = list(dataSet.columns) #提取出数据集所有的列
    classlist = dataSet.iloc[:,-1].value_counts() #获取最后一列类标签

    #判断最多标签数目是否等于数据集行数，或者数据集是否只有一列
    if classlist[0]==dataSet.shape[0] or dataSet.shape[1] == 1:
        return classlist.index[0] #如果是，返回类标签

    axis = bestSplit(dataSet) #确定出当前最佳切分列的索引
    bestfeat = featlist[axis] #获取该索引对应的特征
    myTree = {bestfeat:{}} #采用字典嵌套的方式存储树信息

    del featlist[axis] #删除当前特征

    valuelist = set(dataSet.iloc[:,axis]) #提取最佳切分列所有属性值

    for value in valuelist: #对每一个属性值递归建树
        myTree[bestfeat][value] = createTree(mySplit(dataSet,axis,value))
    return myTree

4. 存储

构造决策树是很耗时的任务，即使处理很小的数据集，也要花费几秒的时间，如果数据集很大，将会耗费很多计算时间。因此为了节省时间，建好树之后立马将其保存，后续使用直接调用即可。

#树的存储
np.save('myTree.npy',myTree)

#树的读取
read_myTree = np.load('myTree.npy').item()
read_myTree

5. 实战

5.1. 导入数据

lenses = pd.read_table('lenses.txt',header = None)
lenses.columns =['age','prescript','astigmatic','tearRate','class']
lenses

5.2. 划分数据

import random

"""
函数功能：切分训练集和测试集
参数说明：
    dataSet:输入的数据集
    rate：训练集所占比例
返回：
    train,test:切分好的训练集和测试集
"""
def randSplit(dataSet, rate):
    l = list(dataSet.index) #提取出索引
    random.shuffle(l) #随机打乱索引
    dataSet.index = l #将打乱后的索引重新赋值给原数据集
    n = dataSet.shape[0] #总行数
    m = int(n * rate) #训练集的数量
    train = dataSet.loc[range(m), :] #提取前m个记录作为训练集
    test = dataSet.loc[range(m, n), :] #剩下的作为测试集
    dataSet.index = range(dataSet.shape[0]) #更新原数据集的索引
    test.index = range(test.shape[0]) #更新测试集的索引
    return train, test

5.3. 生成树

#利用训练集生成决策树
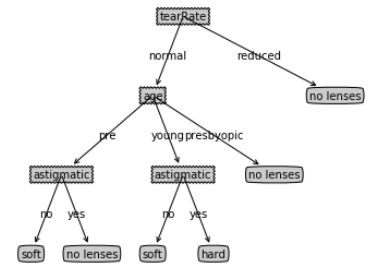
lensesTree = createTree(train1)
lensesTree

#构造注解树
createPlot(lensesTree)

5.4. 分类

#用决策树进行分类并计算有预测准确率
acc_classify(train1,test1)

微信扫一扫分享文章