3D-Genome | Hi-C互作矩阵归一化指南

数据科学工厂

Hi-C 是一种基于测序的方法，用于分析全基因组染色质互作。它已广泛应用于研究各种生物学问题，如基因调控、染色质结构、基因组组装等。Hi-C 实验涉及一系列生物化学反应，可能会在输出中引入噪声。随后的数据分析也会产生影响最终输出噪声：互作矩阵，其中矩阵中的每个元素表示基因组任意两个区域之间的互作强度。因此，Hi-C 数据分析的关键步骤是消除此类噪声，该步骤也称为 Hi-C 数据归一化。

归一化方法

为了归一化 Hi-C matrix，可以采用以下多种方法：

• Iterative Correction (IC) :该方法通过消除实验过程中的偏差来归一化原始接触图。这是一种矩阵平衡的方法，但是，在归一化的情况下，行和列的总和不等于1。
• Knight-Ruiz Matrix Balancing (KR):Knight-Ruiz (KR) 矩阵平衡是一种归一化对称矩阵的快速算法。归一化后获得双随机矩阵。在这个矩阵中，行和列的总和等于一。
• Vanilla-Coverage (VC) :该方法首先用于染色体间图谱。后来 Rao 等人，2014 年将其用于染色体内图谱。这是一种简单的方法，首先将每个元素除以相应行的总和，然后除以相应列的总和。
• Median Contact Frequency Scaling (MCFS):此方法可用于使用两个位置/坐标之间的特定距离的中值接触值来归一化接触图。首先，计算每个距离的中值距离接触频率。随后，观察到的接触频率除以根据两个位置之间的距离获得的中值接触频率。

方法详解

早期的 Hi-C 数据归一化方法主要关注引起噪声的显性因素。切割酶位点、基因组映射、GC 含量等因素使测序读数在基因组中分布不均匀，从而在计算成对互作时引入偏差。根据这些想法，Imakaev 等人提出了一种能够“implicitly”处理所有噪声源的方法。背后的想法实际上非常简单：因为 Hi-C 理论上是一个无偏的实验，所有基因组区域的“visibility”应该是相等的。另一个假设是 Hi-C 实验的所有偏差都是一维且可分解的。基于这些假设，一个解决方案是将原始互作矩阵分解为两个一维偏差和一个行和列之和为相同值的归一化矩阵的乘积。

Imakaev提出的方法在矩阵理论中也称为矩阵平衡。矩阵平衡是一个古老的数学问题，可以追溯到一个世纪前。人们已经开发了许多矩阵平衡方法，包括普通覆盖率 (VC)、Sinkhorn & Knopp (SK) 和 Knight & Ruiz 方法 (KR)。

VC是通过将矩阵的每个元素除以其行和和列和来完成的，以去除每个位点的不同测序覆盖度。 VC可以被认为是SK方法的单次迭代。在SK中，重复执行VC过程，直到所有行和列的总和为相同的值。 S&K 这个过程会收敛。

Rao 等人回顾了所有矩阵平衡方法，并将 KR 方法引入 Hi-C 数据。基于K&R的原始论文，KR方法比SP快几个数量级，这使得它适合平衡高分辨率矩阵。实际上，即使在 10kb 分辨率下，ICE 的 SP 实现也非常快。根据我的经验，ICE 和 KR 之间的速度差异可以忽略不计。然而，KR 有一个缺点，即当矩阵太稀疏时，KR 过程可能无法收敛。在我的研究中，当我使用 Juicer tools 在低测序数据集上生成 KR 归一化矩阵得到了一个空矩阵，这种情况发生了几次。

矩阵平衡的算法其实并不难，我们如何计算 Hi-C 互作矩阵的平衡矩阵呢？下面的Python类中实现了VC和SP方法。对于小矩阵来说，这种实现速度很快。

class HiCNorm(object):
    def __init__(self, matrix):
        self.bias = None
        self.matrix = matrix
        self.norm_matrix = None
        self._bias_var = None

    def iterative_correction(self, max_iter=50):
        mat = np.array(self.matrix, dtype=float)
        row_sum = np.sum(mat, axis=1)
        low_count = np.quantile(row_sum, 0.15)
        mask_row = row_sum < low_count
        mat[mask_row, :] = 0
        mat[:, mask_row] = 0

        self.bias = np.ones(mat.shape[0])
        self._bias_var = []
        x, y = np.nonzero(mat)
        mat_sum = np.sum(mat)

        for i in range(max_iter):
            bias = np.sum(mat, axis=1)
            bias_mean = np.mean(bias[bias > 0])
            bias_var = np.var(bias[bias > 0])
            self._bias_var.append(bias_var)
            bias = bias / bias_mean
            bias[bias == 0] = 1

            mat[x, y] = mat[x, y] / (bias[x]*bias[y])
            new_sum = np.sum(mat)
            mat = mat * (mat_sum / new_sum)

            self.bias = self.bias * bias * np.sqrt(new_sum / mat_sum)

        self.norm_matrix = np.array(self.matrix, dtype=float)
        self.norm_matrix[x, y] = self.norm_matrix[x, y] / (self.bias[x] * self.bias[y])

    def vanilla_coverage(self):
        self.iterative_correction(max_iter=1)

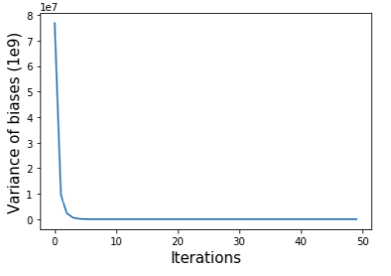
上述算法背后的想法是，我们首先将偏差设置为矩阵每行的总和，并将每个矩阵元素除以其行和列的偏差。重复这两个步骤直到满足收敛标准。我们可以使用偏差的方差（self.bias）来监控平衡过程的收敛性（如下图所示）。

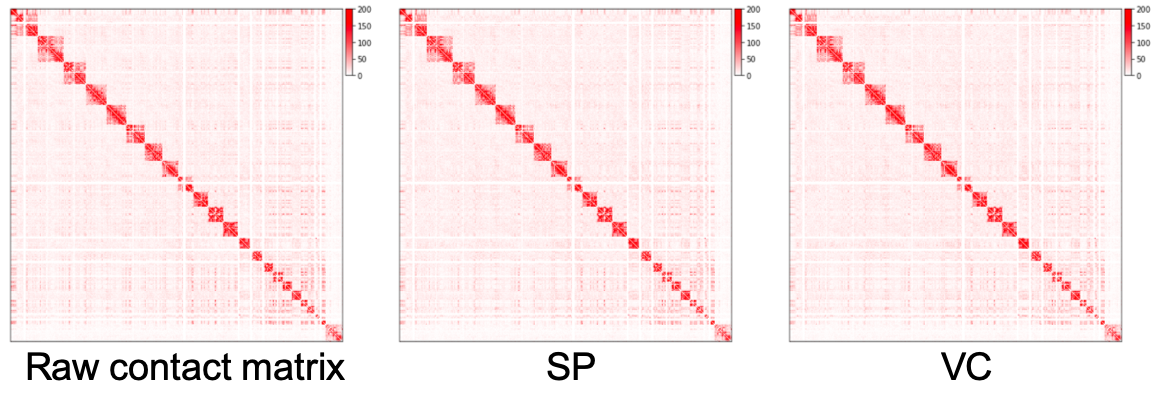
原始互作矩阵、通过 SP 方法和 VC 方法归一化的矩阵绘制为热图，如下所示。我们可以看到，归一化矩阵中远离对角线的区域比原始矩阵更干净，但我们几乎看不到 SP 和 VC 方法之间的差异。在实践中，我们在归一化之前预先过滤具有非常小的值的行。上面的脚本通过将这些行的元素设置为零来过滤掉总和低于所有行总和的 15 分位数的行。

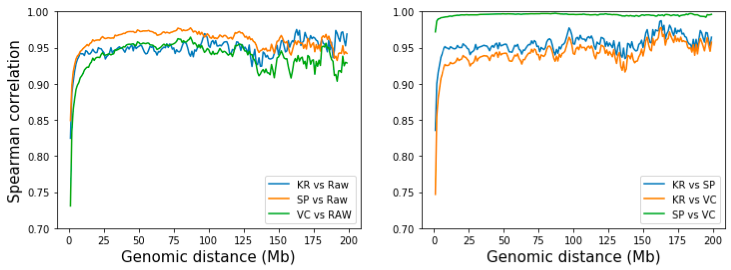
然而，我们可以通过检查相同距离的互作的相关性来量化 SP 和 VC 归一化方法的差异。为此，我们提取并计算两个矩阵的第 d 对角线的相关性，其中 d 是两个基因组区域的距离（在 bin 处）。从下图可以看出，虽然所有三种方法在长距离（>10 Mb）下都类似于原始矩阵，但 SP 与原始矩阵稍微相似。三种方法的成对比较表明，SP 和 VC 高度相似，只是迭代次数不同。 KR 比 VC 更类似于 SP，但差异可以忽略不计。 [注：KR矩阵是用straw API从.hic文件中获得的]。

实际上，Hi-C 归一化仅通过染色体内、仅染色体间或两者来完成。仅对于染色体内，分别在每条染色体上进行 KR 或 ICE。仅对于染色体间，获得全基因组矩阵并从中去除染色体内互作。当包括染色体间相互作用时，高分辨率归一化需要大量内存。因此，归一化通常在全基因组矩阵上以 25kb 或 50kb 分辨率进行。

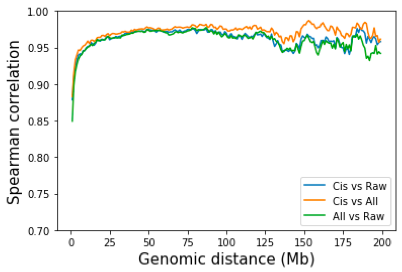
一个自然的问题是，去除染色体间互作是否会对染色体内互作的产生影响？为了回答这个问题，我对所有互作点和仅染色体内互作点进行了 SP 标准化。同样，通过所有互作归一化和仅通过染色体内互作归一化之间的差异非常小。 Juicer tools 和 Cooler 都默认使用所有触点进行归一化。

总结

那么我应该对数据使用哪种归一化方法？

答案可能是这真的不重要。正如 Rao 等人和我们的分析所示，在 VC、ICE(SP)、KR 和其他几种矩阵平衡方法之间观察到高度相关性。 Rao等人在他们的研究中进一步指出，循环调用不受不同归一化方法的影响。他们甚至表明，当对原始数据调用峰值时，循环几乎相同，这让我怀疑我们是否需要矩阵归一化。虽然Rao等人确实提到VC倾向于过度修正互作图并提出VCSQ来补充VC，但我还没有看到有人拿出明确的证据表明KR/ICE优于VC/VCSQ。每种方法的优缺点总结如下：

方法	优点	缺点
VC/VCSQ	快	过度矫正
ICE (SP)	稳健	慢
KR	快，尤其是用于高分辨率	低分辨率不稳定

总之，仍然建议将归一化作为实践的一部分。选择 KR 还是 ICE 在很大程度上取决于您使用的流程（Juicer tools 或 Cooler），但如果您的测序深度相对较低，推荐 ICE，因为它可以保证收敛。

微信扫一扫分享文章