 「一边学习,一边总结,一边分享!」
「一边学习,一边总结,一边分享!」
由于微信改版,一直有同学反映。存在长时间接收不到公众号的推文。那么请跟随以下步骤,将**「小杜的生信筆記」设置为「星标」,不错过每一条推文教程。
写在前面
我们在上一个教程分享了单因素变化差异分析。今天,我们继续来分析多因素差异分析,在日常的分析中,单因素变化差异分析使用频率比较高,对于多因素分析,我们也需进行了解。
注:本文仅是个人学习笔记,若有错误地方,请指出。
多因素差异分析
多因素方差分析(Multifactor Analysis of Variance, ANOVA)是一种用于比较多个因素对一个或多个响应变量的影响的方法。它可以处理多个因子,并能检测因子之间的交互作用
常见的多因素分析类型
- 协方差分析
协方差分析又称带有协变量的方差分析,是一种综合了方差分析和线性回归的重要统计学方法
- 多因素回归模型 当研究中具有多个混杂因素需要考虑时,可根据结局变量类型选择相应的多因素统计学模型进行校正。对于连续型结局变量可考虑多重线性回归;分类型结局变量(包括二分类或多分类)可选择logistic回归;时间事件型结局变量应选择Cox模型;当结局变量为事件发生数时可选择Poisson回归模型。
「(1)多重线性回归」:多重线性回归是研究一个连续型结局变量与多个自变量间线性关系的统计学分析方法。其基本表达形式为Y=β0+β1X1+β2X2+…+βkXk+ε,其中,Y为结局变量;β0为常数项,即截距;β1…βk为各自变量Xj对应的偏回归系数,表示为当其他自变量保持不变时,Xj每变化1个单位,结局变量Y的平均改变量为βj;ε为随机误差。、
「(2)logistic回归:」logistic回归是研究二分类或多分类结局变量与多个影响因素之间关系的多因素回归方法
「(3)Cox回归:」Cox比例风险回归模型简称Cox模型,是针对生存资料的多因素分析方法。
「(4)Poisson回归:」Poisson回归适用于单位时间或空间内某事件(即结局变量)发生次数的影响因素分析。
以上来自https://mp.weixin.qq.com/s/830K8Bik561wY2jcD\_a6wA.
若是从变量的数量来分类,可以分为以下几种:
- 双因素方差分析(Two-way ANOVA)
- 三因素方差分析(Three-way ANOVA)
- 多因素方差分析(Multi-way ANOVA)
- 重复测量方差分析(Repeated Measures ANOVA)
- 协方差分析(ANCOVA)
使用R语言进行分析
- 双因素方差分析(Two-way ANOVA)
# 加载必要的包
library(ggplot2)
library(dplyr)
# 生成示例数据
set.seed(123)
data <- data.frame(
TeachingMethod = factor(rep(c("Traditional", "Experimental"), each = 20)),
Gender = factor(rep(c("Male", "Female"), times = 20)),
Score = rnorm(40, mean = 75, sd = 10)
)
# 进行双因素方差分析
fit <- aov(Score ~ TeachingMethod * Gender, data = data)
# 显示结果
summary(fit)
> summary(fit)
Df Sum Sq Mean Sq F value Pr(>F)
TeachingMethod 137.237.200.4400.511
Gender 126.826.830.3170.577
TeachingMethod:Gender 134.934.930.4130.524
Residuals 363044.584.57
- 三因素方差分析
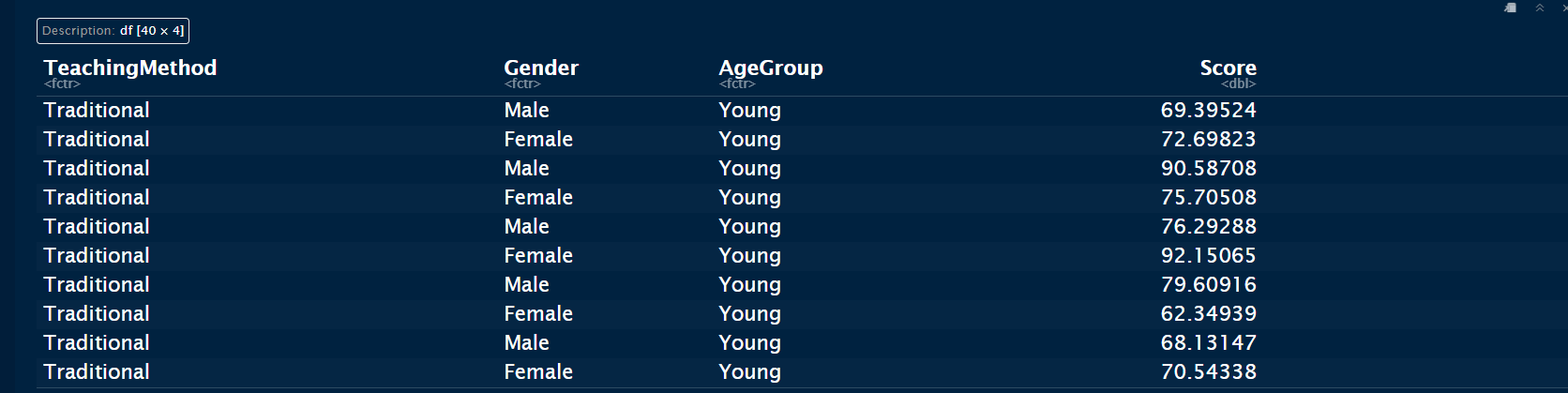
# 生成示例数据
set.seed(123)
data <- data.frame(
TeachingMethod = factor(rep(c("Traditional", "Experimental"), each = 20)),
Gender = factor(rep(c("Male", "Female"), times = 20)),
AgeGroup = factor(rep(c("Young", "Old"), each = 10, times = 2)),
Score = rnorm(40, mean = 75, sd = 10)
)
# 进行三因素方差分析
fit <- aov(Score ~ TeachingMethod * Gender * AgeGroup, data = data)
# 显示结果
summary(fit)
> summary(fit)
Df Sum Sq Mean Sq F value Pr(>F)
TeachingMethod 137.237.200.4420.511
Gender 126.826.830.3190.576
AgeGroup 1193.9193.862.3050.139
TeachingMethod:Gender 134.934.930.4150.524
TeachingMethod:AgeGroup 193.893.821.1160.299
Gender:AgeGroup 156.456.360.6700.419
TeachingMethod:Gender:AgeGroup 19.69.620.1140.737
Residuals 322690.884.09
- 重复测量方差分析
# 安装并加载必要的包
library(nlme)
# 生成示例数据
set.seed(123)
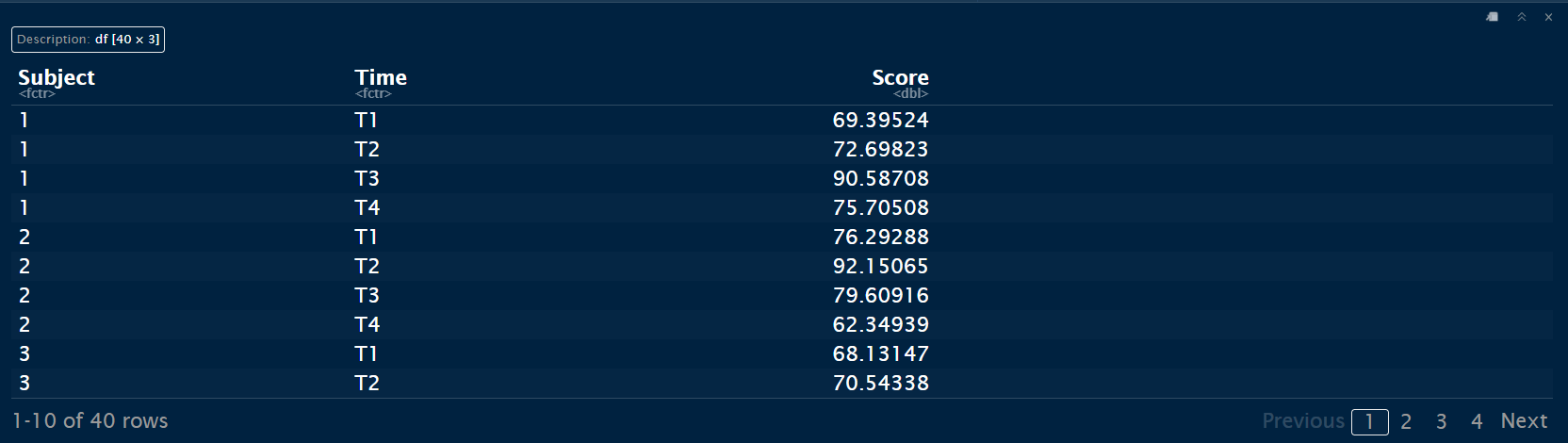
data <- data.frame(
Subject = factor(rep(1:10, each = 4)),
Time = factor(rep(c("T1", "T2", "T3", "T4"), times = 10)),
Score = rnorm(40, mean = 75, sd = 10)
)
data
# 进行重复测量方差分析
fit <- lme(Score ~ Time, random = ~1 | Subject, data = data)
# 显示结果
summary(fit)
anova(fit)

- 协方差分析
# 生成示例数据
set.seed(123)
data <- data.frame(
TeachingMethod = factor(rep(c("Traditional", "Experimental"), each = 20)),
InitialScore = rnorm(40, mean = 70, sd = 10),
FinalScore = rnorm(40, mean = 75, sd = 10)
)
# 进行协方差分析
fit <- aov(FinalScore ~ TeachingMethod + InitialScore, data = data)
# 显示结果
summary(fit)

在实际案例中的分析
多重线性回归
 「结果解释:」
「结果解释:」
- 实际值与预测值的散点图:
1. 图中点应接近红色拟合线,说明模型预测效果较好。
2. 偏离较大的点可能是异常值。
若我们的教程对你有所帮助,请点赞+收藏+转发,这是对我们最大的支持。
往期部分文章
「1. 最全WGCNA教程(替换数据即可出全部结果与图形)」
「2. 精美图形绘制教程」
「3. 转录组分析教程」
「4. 转录组下游分析」
「小杜的生信筆記」 ,主要发表或收录生物信息学教程,以及基于R分析和可视化(包括数据分析,图形绘制等);分享感兴趣的文献和学习资料!!